Weights are created in NHANES to account for the complex survey design (including oversampling), survey non-response, and post-stratification adjustment to match total population counts from the Census Bureau. When a sample is weighted in NHANES it is representative of the U.S. civilian noninstitutionalized resident population. A sample weight is assigned to each sample person. It is a measure of the number of people in the population represented by that sample person.
How weights are created in the Continuous NHANES
The sample weight is created in three steps:
- the base weight is computed, which accounts for the unequal probabilities of selection given that some demographic groups were over-sampled;
- adjustments are made for non-response; and
- post-stratification adjustments are made to match estimates of the U.S. civilian non-institutionalized population available from the Census Bureau.
1. Calculation of the base weight
In general a sample person is assigned a weight that is equivalent to the reciprocal of his/her probability of selection. In other words:
$$\text{Sample person's weight} = \frac{1}{\text{probability of selection}}$$
However, calculating the base weight for a sample person in NHANES is much more complicated due to the survey's complex, multistage design. In NHANES, the following equation, which takes into account the survey design, is used to determine the base weight for a sample person:
$$\text{Base weight} = \frac{1}{\text{final probability}}$$
where
$$\begin{align*} \text{Final probability} =&\big(\Pr(\text{PSU is selected}) \\
&\times \Pr(\text{segment of the PSU is selected}) \\
&\times \Pr(\text{household is selected}) \\
&\times \Pr(\text{individual is selected})\big) \end{align*}$$
IMPORTANT NOTE
The NHANES sample weights can be quite variable due to the oversampling of subgroups. For estimates by age and race and Hispanic origin, use of the following age categories is recommended for reducing the variability in the sample weights and therefore reducing the variance of the estimates: 5 years and under, 6-11 years, 12-19 years, 20-39 years, 40-59 years, 60 years and over.
2. Adjustment for nonresponse
Adjustment for nonresponse to the interview or exam
The base weights were adjusted for nonresponse to the in-home interview when creating interview weights and further adjusted for non-response to the MEC exam when creating exam weights.
In NHANES, an individual can be classified as a non-respondent to the interview portion of the survey and/or the exam portion. An individual is considered a non-respondent to the interview if he/she was selected to be in the sample, but did not participate in the in-home interview. Similarly, an individual who completed the interview but did not agree to, or come in for, the MEC portion of the survey is considered a non-respondent to the exam. Adjustments made for survey non-response account only for sample person interview or exam non-response, but not for item non-response (i.e., a sample person declined to have their blood pressure measured in the examination component but completed all other examination components).
Response rates by age and sex for all cycles of Continuous NHANES can be downloaded from the NHANES response rates website.
Adjustment for nonresponse to NHANES subsample components
NHANES respondents are asked to participate in a variety of survey components that are statistically defined (or random) subsamples of the NHANES MEC-examined sample. These include a variety of lab, nutrition/dietary, environmental, or mental health components. (Please see the respective survey protocol/documentation for more specific information.) For example, participants who were selected to schedule their MEC exam in a morning session (half of all examined participants) were asked to give a fasting blood sample. The subsamples selected for these components are chosen at random with a specified sampling fraction (for example, 1/2 or 1/3 of the total examined group) according to the protocol for that component. Each component subsample has its own designated weight, which accounts for the additional probability of selection into the subsample component, as well as an additional adjustment for component nonresponse.
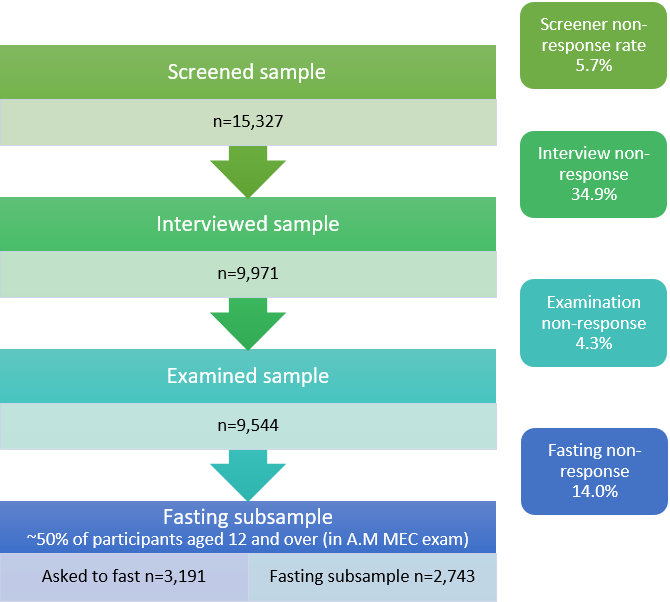
Diagram of Nonresponse Rates for NHANES 2015-2016
* Unweighted response rates = [(Unweighted sample size) / (Screener sample size)] × (the screener response rate: 94.3%)
The diagram above demonstrates the varying levels of sampling nonresponse. In the example above, the selected sample included a total of 15,327 sample persons for the years 2015–2016. Only 9,971 of those sample persons actually completed the in-home interview. Therefore 34.9% of the individuals sampled did not complete the in-home interview. This is interview nonresponse. In 2015–2016, because the screener response rate was lower than 98%, the unweighted response rate for the interviewed sample was adjusted to incorporate non-response at the screener level. The unweighted response rate for the interviewed sample was 61.3%.
Among the 9,971 sample persons who were interviewed, only 9,544 completed the MEC exam. Therefore an additional 4.3% of the interviewed sample persons did not respond to the MEC exam. This is the MEC exam nonresponse. The unweighted response rate for the examined sample, adjusted for non-response at the screener level, was 58.7%.
This example also shows the additional subsampling for the AM fasting blood sample. Approximately 50% of MEC participants aged 12 and over (3,191 persons) were partitioned to fast for 9 hours and come to the morning MEC exam. Of the 3,191 persons partitioned to the morning subsample, only 2,743 actually fasted, so the morning fasting sample was adjusted for the additional 14.0% nonresponse to the morning fast.
3. Post-stratification adjustment to match population control totals from the U.S. Census Bureau
In addition to accounting for sample person non-response, weights are also post-stratified to match the population control totals for each sampling subdomain. This additional adjustment makes the weighted counts the same as an independent estimate of the noninstitutionalized civilian population of the United States.
For NHANES 2011-2016, the sample weights were post-stratified to population totals obtained from the American Community Survey (ACS). The weights for earlier NHANES cycles were post-stratified to population totals from the Current Population Survey (CPS). This change from the CPS to the ACS was made, in part, because the larger sample size of the ACS could provide more reliable population estimates for Asian persons within age and sex categories, which was required due to the addition of the Asian oversample in the 2011 survey.
The population controls totals (by sex, age, and race and Hispanic origin domains) used for each NHANES cycle are available on the NHANES Response Rates and Population Totals page.
Summary
The sample weights are created to account for the complex survey design (including oversampling), survey nonresponse, and post-stratification in order to ensure that calculated estimates are representative of the U.S. civilian noninstitutionalized population. More information about how the NHANES weights are created can be found in the Estimation Procedures documents on the NHANES website.